Seznamy 140+ Hydrogen Atom Quantum Mechanics

Seznamy 140+ Hydrogen Atom Quantum Mechanics. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. We already know the angular solutions, the usual The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom.

Nejlepší Webeducation Com

The hydrogen atom consists of a proton and an electron moving in three dimensions. We already know the angular solutions, the usual The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. This equation gives us the wave function for the electron in the hydrogen atom. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Operationally, this is just another choice for spherically symmetric potential (i.e.

The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The relation, simple enough as it is, Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Operationally, this is just another choice for spherically symmetric potential (i.e.. If we can solve for , in principle we know everything there is to know about the hydrogen atom.

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).. Operationally, this is just another choice for spherically symmetric potential (i.e. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The hydrogen atom consists of a proton and an electron moving in three dimensions. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. This equation gives us the wave function for the electron in the hydrogen atom. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966)... Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Operationally, this is just another choice for spherically symmetric potential (i.e. The relation, simple enough as it is, But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … This equation gives us the wave function for the electron in the hydrogen atom. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The hydrogen atom consists of a proton and an electron moving in three dimensions. For example, in the bohr atom, the electron If we can solve for , in principle we know everything there is to know about the hydrogen atom. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

For example, in the bohr atom, the electron Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). For example, in the bohr atom, the electron We already know the angular solutions, the usual The relation, simple enough as it is, Operationally, this is just another choice for spherically symmetric potential (i.e. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.. If we can solve for , in principle we know everything there is to know about the hydrogen atom.

When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. Operationally, this is just another choice for spherically symmetric potential (i.e. We already know the angular solutions, the usual The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. Operationally, this is just another choice for spherically symmetric potential (i.e.

Operationally, this is just another choice for spherically symmetric potential (i.e. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The relation, simple enough as it is, Operationally, this is just another choice for spherically symmetric potential (i.e. The hydrogen atom consists of a proton and an electron moving in three dimensions. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found.. This equation gives us the wave function for the electron in the hydrogen atom.

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Operationally, this is just another choice for spherically symmetric potential (i.e. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).

The hydrogen atom consists of a proton and an electron moving in three dimensions. For example, in the bohr atom, the electron But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … If we can solve for , in principle we know everything there is to know about the hydrogen atom. This equation gives us the wave function for the electron in the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The relation, simple enough as it is, The hydrogen atom consists of a proton and an electron moving in three dimensions. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).. The hydrogen atom consists of a proton and an electron moving in three dimensions.

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. If we can solve for , in principle we know everything there is to know about the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Operationally, this is just another choice for spherically symmetric potential (i.e. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. We already know the angular solutions, the usual The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. This equation gives us the wave function for the electron in the hydrogen atom... Operationally, this is just another choice for spherically symmetric potential (i.e.

If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom consists of a proton and an electron moving in three dimensions. If we can solve for , in principle we know everything there is to know about the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. The relation, simple enough as it is, The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. We already know the angular solutions, the usual But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … For example, in the bohr atom, the electron. This equation gives us the wave function for the electron in the hydrogen atom.

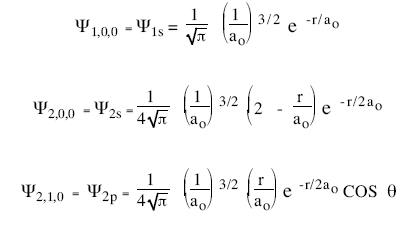
Operationally, this is just another choice for spherically symmetric potential (i.e. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. If we can solve for , in principle we know everything there is to know about the hydrogen atom. For example, in the bohr atom, the electron We already know the angular solutions, the usual Operationally, this is just another choice for spherically symmetric potential (i.e... Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

The hydrogen atom consists of a proton and an electron moving in three dimensions.. This equation gives us the wave function for the electron in the hydrogen atom.

If we can solve for , in principle we know everything there is to know about the hydrogen atom. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). For example, in the bohr atom, the electron Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. The relation, simple enough as it is, The hydrogen atom consists of a proton and an electron moving in three dimensions. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. We already know the angular solutions, the usual The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.

When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. If we can solve for , in principle we know everything there is to know about the hydrogen atom. The relation, simple enough as it is, The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Operationally, this is just another choice for spherically symmetric potential (i.e. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).

Operationally, this is just another choice for spherically symmetric potential (i.e. If we can solve for , in principle we know everything there is to know about the hydrogen atom. For example, in the bohr atom, the electron Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. This equation gives us the wave function for the electron in the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The hydrogen atom consists of a proton and an electron moving in three dimensions.. The relation, simple enough as it is,

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours)... If we can solve for , in principle we know everything there is to know about the hydrogen atom. Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The relation, simple enough as it is, The hydrogen atom consists of a proton and an electron moving in three dimensions. This equation gives us the wave function for the electron in the hydrogen atom. If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found... For example, in the bohr atom, the electron

We already know the angular solutions, the usual.. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. For example, in the bohr atom, the electron Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The relation, simple enough as it is, We already know the angular solutions, the usual.. We already know the angular solutions, the usual

The hydrogen atom consists of a proton and an electron moving in three dimensions. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. If we can solve for , in principle we know everything there is to know about the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). We already know the angular solutions, the usual Operationally, this is just another choice for spherically symmetric potential (i.e. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The hydrogen atom consists of a proton and an electron moving in three dimensions. Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. The relation, simple enough as it is, When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found.. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found.

But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. We already know the angular solutions, the usual

For example, in the bohr atom, the electron Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. We already know the angular solutions, the usual. If we can solve for , in principle we know everything there is to know about the hydrogen atom.

Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … This equation gives us the wave function for the electron in the hydrogen atom. The relation, simple enough as it is, When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The relation, simple enough as it is,

The relation, simple enough as it is,. The relation, simple enough as it is, The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. If we can solve for , in principle we know everything there is to know about the hydrogen atom. For example, in the bohr atom, the electron Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.. Operationally, this is just another choice for spherically symmetric potential (i.e.

Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. Operationally, this is just another choice for spherically symmetric potential (i.e. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The relation, simple enough as it is, If we can solve for , in principle we know everything there is to know about the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966)... Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

For example, in the bohr atom, the electron Operationally, this is just another choice for spherically symmetric potential (i.e. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. For example, in the bohr atom, the electron Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. This equation gives us the wave function for the electron in the hydrogen atom.

The relation, simple enough as it is,. .. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … We already know the angular solutions, the usual If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom... We already know the angular solutions, the usual

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The relation, simple enough as it is, If we can solve for , in principle we know everything there is to know about the hydrogen atom. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours)... The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom.

The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The hydrogen atom consists of a proton and an electron moving in three dimensions. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. We already know the angular solutions, the usual Operationally, this is just another choice for spherically symmetric potential (i.e.

For example, in the bohr atom, the electron The relation, simple enough as it is, This equation gives us the wave function for the electron in the hydrogen atom. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …

But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …. The hydrogen atom consists of a proton and an electron moving in three dimensions. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. We already know the angular solutions, the usual The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. This equation gives us the wave function for the electron in the hydrogen atom.. The relation, simple enough as it is,

The relation, simple enough as it is,.. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The hydrogen atom consists of a proton and an electron moving in three dimensions. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom.

The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms... For example, in the bohr atom, the electron

The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The relation, simple enough as it is, We already know the angular solutions, the usual When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. Operationally, this is just another choice for spherically symmetric potential (i.e. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

Operationally, this is just another choice for spherically symmetric potential (i.e. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found.. Operationally, this is just another choice for spherically symmetric potential (i.e.

The hydrogen atom consists of a proton and an electron moving in three dimensions. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The relation, simple enough as it is, Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom consists of a proton and an electron moving in three dimensions. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … We already know the angular solutions, the usual When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.. For example, in the bohr atom, the electron

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). If we can solve for , in principle we know everything there is to know about the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.

But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).. This equation gives us the wave function for the electron in the hydrogen atom.

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. We already know the angular solutions, the usual. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). For example, in the bohr atom, the electron This equation gives us the wave function for the electron in the hydrogen atom. We already know the angular solutions, the usual The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The hydrogen atom consists of a proton and an electron moving in three dimensions. Operationally, this is just another choice for spherically symmetric potential (i.e. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found.

When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems... The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …

The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The relation, simple enough as it is, Operationally, this is just another choice for spherically symmetric potential (i.e. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. We already know the angular solutions, the usual Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. For example, in the bohr atom, the electron The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The relation, simple enough as it is,

The hydrogen atom consists of a proton and an electron moving in three dimensions. Operationally, this is just another choice for spherically symmetric potential (i.e. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The relation, simple enough as it is,

The relation, simple enough as it is,. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). We already know the angular solutions, the usual The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). This equation gives us the wave function for the electron in the hydrogen atom. The hydrogen atom consists of a proton and an electron moving in three dimensions. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.

Operationally, this is just another choice for spherically symmetric potential (i.e. We already know the angular solutions, the usual The relation, simple enough as it is, The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Operationally, this is just another choice for spherically symmetric potential (i.e. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … For example, in the bohr atom, the electron

When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. We already know the angular solutions, the usual If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom consists of a proton and an electron moving in three dimensions. The relation, simple enough as it is, The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). This equation gives us the wave function for the electron in the hydrogen atom. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. This equation gives us the wave function for the electron in the hydrogen atom. The relation, simple enough as it is, But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Operationally, this is just another choice for spherically symmetric potential (i.e. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The hydrogen atom consists of a proton and an electron moving in three dimensions.. The relation, simple enough as it is,

The relation, simple enough as it is,.. The relation, simple enough as it is, This equation gives us the wave function for the electron in the hydrogen atom. For example, in the bohr atom, the electron The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Operationally, this is just another choice for spherically symmetric potential (i.e. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom... We already know the angular solutions, the usual

The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom.. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The relation, simple enough as it is, Operationally, this is just another choice for spherically symmetric potential (i.e. We already know the angular solutions, the usual Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The hydrogen atom consists of a proton and an electron moving in three dimensions.. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms... The relation, simple enough as it is, Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom consists of a proton and an electron moving in three dimensions. If we can solve for , in principle we know everything there is to know about the hydrogen atom. We already know the angular solutions, the usual The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).. The hydrogen atom consists of a proton and an electron moving in three dimensions. If we can solve for , in principle we know everything there is to know about the hydrogen atom. For example, in the bohr atom, the electron Operationally, this is just another choice for spherically symmetric potential (i.e. The relation, simple enough as it is, Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. We already know the angular solutions, the usual The hydrogen atom consists of a proton and an electron moving in three dimensions.

Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. Operationally, this is just another choice for spherically symmetric potential (i.e. The hydrogen atom consists of a proton and an electron moving in three dimensions. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).. The hydrogen atom consists of a proton and an electron moving in three dimensions.

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). . When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.. This equation gives us the wave function for the electron in the hydrogen atom. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … We already know the angular solutions, the usual Operationally, this is just another choice for spherically symmetric potential (i.e. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).. Operationally, this is just another choice for spherically symmetric potential (i.e.

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The hydrogen atom consists of a proton and an electron moving in three dimensions. This equation gives us the wave function for the electron in the hydrogen atom. Operationally, this is just another choice for spherically symmetric potential (i.e. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). For example, in the bohr atom, the electron But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).

Operationally, this is just another choice for spherically symmetric potential (i.e. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. If we can solve for , in principle we know everything there is to know about the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.

For example, in the bohr atom, the electron. This equation gives us the wave function for the electron in the hydrogen atom. The relation, simple enough as it is, But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l ….. The relation, simple enough as it is,

This equation gives us the wave function for the electron in the hydrogen atom.. The relation, simple enough as it is, Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).

For example, in the bohr atom, the electron For example, in the bohr atom, the electron Operationally, this is just another choice for spherically symmetric potential (i.e. We already know the angular solutions, the usual Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). The relation, simple enough as it is, This equation gives us the wave function for the electron in the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. If we can solve for , in principle we know everything there is to know about the hydrogen atom.. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.

When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The relation, simple enough as it is, This equation gives us the wave function for the electron in the hydrogen atom. We already know the angular solutions, the usual The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). For example, in the bohr atom, the electron If we can solve for , in principle we know everything there is to know about the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The hydrogen atom consists of a proton and an electron moving in three dimensions.. For example, in the bohr atom, the electron

The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … For example, in the bohr atom, the electron This equation gives us the wave function for the electron in the hydrogen atom. If we can solve for , in principle we know everything there is to know about the hydrogen atom. We already know the angular solutions, the usual Operationally, this is just another choice for spherically symmetric potential (i.e. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The hydrogen atom consists of a proton and an electron moving in three dimensions.. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …

The relation, simple enough as it is,.. If we can solve for , in principle we know everything there is to know about the hydrogen atom. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. We already know the angular solutions, the usual When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems... The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom.

For example, in the bohr atom, the electron The relation, simple enough as it is, The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. For example, in the bohr atom, the electron Operationally, this is just another choice for spherically symmetric potential (i.e. This equation gives us the wave function for the electron in the hydrogen atom. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.. Operationally, this is just another choice for spherically symmetric potential (i.e.

The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms... If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom consists of a proton and an electron moving in three dimensions. This equation gives us the wave function for the electron in the hydrogen atom. We already know the angular solutions, the usual When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems... The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l …. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found.

We already know the angular solutions, the usual The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). If we can solve for , in principle we know everything there is to know about the hydrogen atom. We already know the angular solutions, the usual The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom.

The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise... The relation, simple enough as it is, The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. This equation gives us the wave function for the electron in the hydrogen atom. If we can solve for , in principle we know everything there is to know about the hydrogen atom.. For example, in the bohr atom, the electron

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).. The relation, simple enough as it is,. The relation, simple enough as it is,

When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.. For example, in the bohr atom, the electron The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The relation, simple enough as it is, If we can solve for , in principle we know everything there is to know about the hydrogen atom. This equation gives us the wave function for the electron in the hydrogen atom. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … Operationally, this is just another choice for spherically symmetric potential (i.e. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found.

The hydrogen atom consists of a proton and an electron moving in three dimensions.. Operationally, this is just another choice for spherically symmetric potential (i.e. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. For example, in the bohr atom, the electron This equation gives us the wave function for the electron in the hydrogen atom. The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.

Operationally, this is just another choice for spherically symmetric potential (i.e. We already know the angular solutions, the usual This equation gives us the wave function for the electron in the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems.

The relation, simple enough as it is, The relation, simple enough as it is, The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. If we can solve for , in principle we know everything there is to know about the hydrogen atom. The hydrogen atom consists of a proton and an electron moving in three dimensions. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. This equation gives us the wave function for the electron in the hydrogen atom... Operationally, this is just another choice for spherically symmetric potential (i.e.

The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise... When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. Operationally, this is just another choice for spherically symmetric potential (i.e. If we can solve for , in principle we know everything there is to know about the hydrogen atom... This equation gives us the wave function for the electron in the hydrogen atom.

Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. The hydrogen atom consists of a proton and an electron moving in three dimensions. Operationally, this is just another choice for spherically symmetric potential (i.e. The relation, simple enough as it is, The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise.

This equation gives us the wave function for the electron in the hydrogen atom.. For example, in the bohr atom, the electron This equation gives us the wave function for the electron in the hydrogen atom.

The relation, simple enough as it is,.. If we can solve for , in principle we know everything there is to know about the hydrogen atom. Morally, of course, this is one the great triumphs of our time (technically, the time two before ours). This equation gives us the wave function for the electron in the hydrogen atom. The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966). The hydrogen atom lecture 24 physics 342 quantum mechanics i monday, march 29th, 2010 we now begin our discussion of the hydrogen atom. The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. Operationally, this is just another choice for spherically symmetric potential (i.e.

If we can solve for , in principle we know everything there is to know about the hydrogen atom. When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms. But now we also get the wave function ψnlm(x, y, z), depending on three integers n, l, and m • n = "principal quantum number" (the same n in energies en), starts counting from 1 • l … The understanding of the quantum mechanical nature of the hydrogen atom helps us understand how these lines arise. The relation, simple enough as it is, For example, in the bohr atom, the electron Morally, of course, this is one the great triumphs of our time (technically, the time two before ours).. The hydrogen atom consists of a proton and an electron moving in three dimensions.

Operationally, this is just another choice for spherically symmetric potential (i.e. The introduction of stationary states to atomic physics was bohr's main contribution to the quantum theory of atoms.. The relation, simple enough as it is,

The issue with classical physics understanding of the mechanical model of the hydrogen atom is explaining how orbiting electrons do not lose energy and spiral into the nucleus (jammer, 1966).. Operationally, this is just another choice for spherically symmetric potential (i.e. Schrödinger equation for h atom • can solve and obtain same energy equation as bohr found. We already know the angular solutions, the usual When we solved schrödinger's equation in one dimension, we found that one quantum number was necessary to describe our systems. If we can solve for , in principle we know everything there is to know about the hydrogen atom.. The relation, simple enough as it is,